Gợi ý đáp án và nhận định đề thi Toán vào lớp 10 tại TP.HCM

Năm nay, TP.HCM có 94.000 thí sinh đăng ký dự thi lớp 10 công lập. Trong số này, hơn 86.000 thí sinh thi lớp 10 thường, khoảng 6.400 thí sinh dự thi chuyên, 1.300 thí sinh dự thi lớp 10 tích hợp.

Hôm qua, các thí sinh đã làm bài thi môn Văn và Ngoại ngữ. Sau ngày thi đầu tiên, 660 thí sinh bỏ thi do bị ốm hoặc không thực sự muốn thi vào trường công lập.

Nhận định chung về đề Toán năm nay, thầy cô trong Tổ Toán - Hệ thống giáo dục HOCMAI cho biết đề thi tuyển sinh vào lớp 10 môn Toán của Sở Giáo dục và Đào tạo TP.HCM năm học 2022-2023 giữ được tính ổn định về cấu trúc so với năm 2020-2021 đồng thời các yêu cầu về kiến thức và kĩ năng đã được giảm nhẹ để phù hợp với tình hình học tập thực tế của học sinh (học trực tuyến gần hết học kỳ I).

Đề thi gồm 8 bài toán lớn và có tính ứng dụng thực tế cao, tiệm cận với xu hướng học Toán chung trên thế giới. Mỗi bài gồm nhiều ý nhỏ với cấu trúc điểm ổn định và được sắp xếp theo thứ tự từ dễ đến khó.

Về phạm vi kiến thức và độ khó

So với đề thi năm 2020-2021, đề năm 2022-2023 có cấu trúc tương đồng và có sự giảm nhẹ về độ khó. Nội dung đề thi nằm trong chương trình THCS và không chứa kiến thức tinh giản của Bộ Giáo dục và Đào tạo. Bài số 7 (ý b) là bài tập khó nhằm đánh giá khả năng lập luận, tư duy logic của học sinh và đây là câu hỏi mang tính chất phân loại thí sinh. Nhận định cụ thể về từng câu hỏi trong đề như sau:

· Bài 1, 2: có dạng thức quen thuộc, ở mức cơ bản, thí sinh có thể hoàn thành tốt. Bài số 2 liên quan đến ứng dụng của định lí Vi-et đã giảm về độ khó so với năm 2020-2021, giảm bớt các bước biến đổi để áp dụng định lí.

· Bài 3: là dạng bài cho biểu thức biểu diễn mối quan hệ giữa các đại lượng, có yếu tố thực tiễn (chỉ số BMI). Học sinh cần đọc hiểu các dữ kiện trong đề bài để tìm được hướng làm bài. Dạng toán đề bài cho sẵn công cụ và công thức tính, thí sinh chỉ cần hiểu và áp dụng công thức để giải toán mà không cần phải ghi nhớ. Đây là một xu hướng ra đề hiện đại giảm bớt sự ghi nhớ về mặt công thức mà coi trọng kiểm tra tính tư duy và kĩ năng đọc hiểu. Và độ khó của câu hỏi này cũng giảm hẳn so với năm 2020, không yêu cầu quá nhiều về kĩ năng đọc hiểu và phân tích đề bài.

· Bài 4: là câu hỏi có tính thực tế. Thí sinh chỉ cần đọc kĩ và phân tích các dữ kiện của đề bài là có thể hoàn thành. Ngoài ra, từ các dữ kiện đã cho của đề bài thí sinh cần lập luận chặt chẽ để rút ra được phép tính đúng, từ đó rút ra kết luận của bài toán.

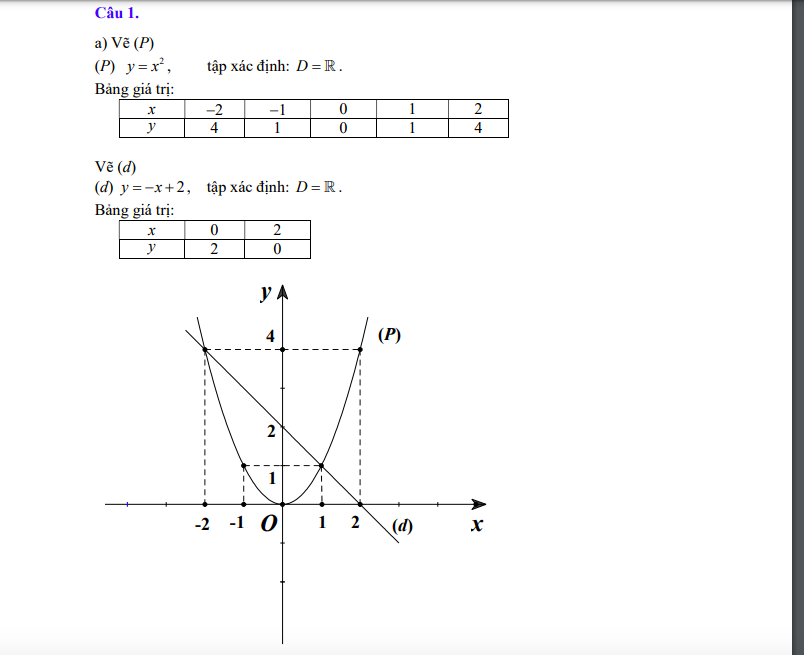
· Bài 5: Đây là dạng bài thực tế có liên quan đến hàm số bậc nhất (tương tự bài 4 của đề thi năm 2020). Các dữ kiện đề bài đưa ra rất cụ thể và tường minh, vì vậy các thí sinh chỉ cần nắm vững kiến thức về hàm số bậc nhất là dễ dàng tìm ra được kết quả của bài toán.

· Bài 6: là bài toán về hình học không gian. Trong ý a, đề bài đã cho sẵn các công thức và học sinh chỉ cần áp dụng đúng công thức là tìm ra kết quả. Trong ý b, học sinh cần vận dụng công thức về thể tích khối hộp chữ nhật kết hợp với các dữ kiện của đề bài là dễ dàng tìm ra đáp số.

· Bài 7: Đây là bài toán nhằm đánh giá tư duy logic của thí sinh và là một dạng bài mới với học sinh vì vậy, để giải quyết được bài toán này, đòi hỏi học sinh phải có tư duy rõ ràng, mạch lạc và khả năng phân tích, lập luận tốt.

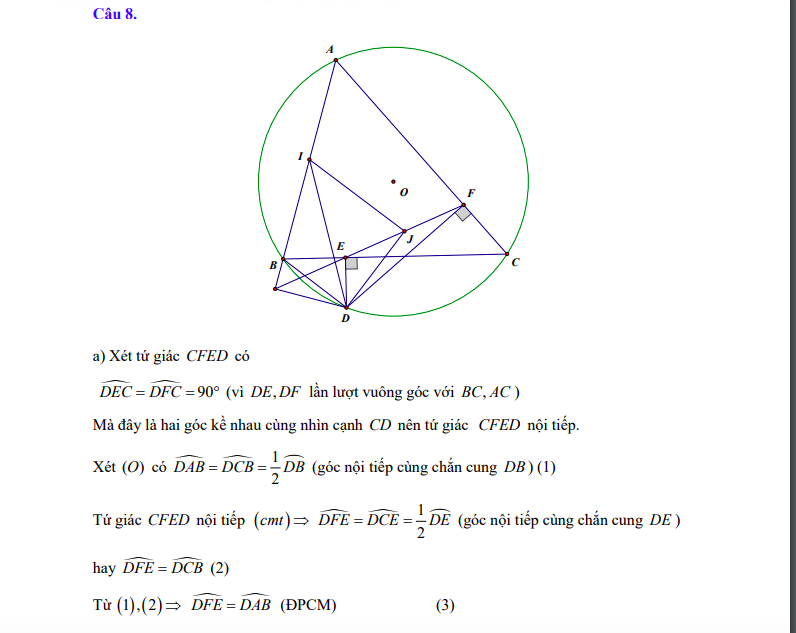
· Bài 8: Đây là dạng bài liên quan đến tứ giác nội tiếp, các bài toán chứng minh góc bằng nhau, chứng minh đẳng thức, chứng minh vuông góc.

Kết luận: Nhìn chung, đề thi năm 2022-2023 về cơ bản không có sự thay đổi so với năm 2020-2021. Cấu trúc bài thi hướng đến đánh giá năng lực toàn diện của người học, áp dụng các kiến thức toán học để giải các bài toán trong thực tế và rất thời sự. Đồng thời, đề thi có câu hỏi chứa vấn đề toán học có nội dung kiến thức tiệm cận với nội dung kiến thức của chương trình giáo dục phổ thông mới 2018 (bài 7).

Đề bài dài nhưng khá hợp lý. Đề thi giảm về độ khó của câu hỏi cho phù hợp với thực tế học tập của học sinh trong suốt gần 1 năm qua.

Đáp án đề thi vào lớp 10 TP.HCM năm 2022 - 2023 môn Toán, tổ chức thi sáng chủ nhật ngày 12/6 được các thầy cô trong Tổ Toán - Hệ thống giáo dục HOCMAI gợi ý giải như sau:

Hoàng Thanh